Math Bytes

A deep learning U-Net model that classifies damaged automobiles | View Code

"Machine intelligence is the last invention that humanity will ever need to make."

- Nick Bostrom

Computer Science 474

When my Deep Learning professor announced that he was replacing our final exam with a project of our choice, I immediately knew the program I wanted to tackle. I had been working on Casper, a used car web scraping program for months, but consistently ran into a challenge - the cars Casper marked as "best deals" were often damaged, and sometimes severely so. A human could easily spot the damage in the picture of the vehicle on the website, but I wanted to create a fully automated process for detecting these types of sales. In the final weeks of the semester, I devoted over 30 hours to developing my first independent deep learning model from start to finish.

Deep Learning

Deep learning is a powerful subset of artificial intelligence that enables computers to learn and make decisions by processing vast amounts of data. In the context of computer vision for detecting damaged vehicles, deep learning algorithms can automatically analyze images or videos to identify signs of vehicle damage. By training on large datasets of labeled images, deep learning models can learn complex patterns and features specific to damaged vehicles. These models employ neural networks with multiple layers to extract hierarchical representations of the input data, allowing them to automatically learn and adapt to new data. This capability makes it an invaluable tool in the field of computer vision, especially as I worked on identifying and assessing damaged vehicles efficiently and reliably.

Data Analysis

In my quest to create a robust deep learning model for car damage detection and price prediction, I scoured the internet for relevant and available databases. After sifting through numerous options, I compiled a dataset of nearly 3,000 images. I scraped about half by myself from various online retailers, but the other half I found from pre-made datasets by Stanford and Roboflow. The images I scraped were from online used car retailers like AutoTrader using Selenium.

After building this dataset however, I discovered a significant issue with the annotations in the pre-made datasets, leading to a mismatch of information.I addressed this issue by removing location annotations and marking entire images as damaged or undamaged.

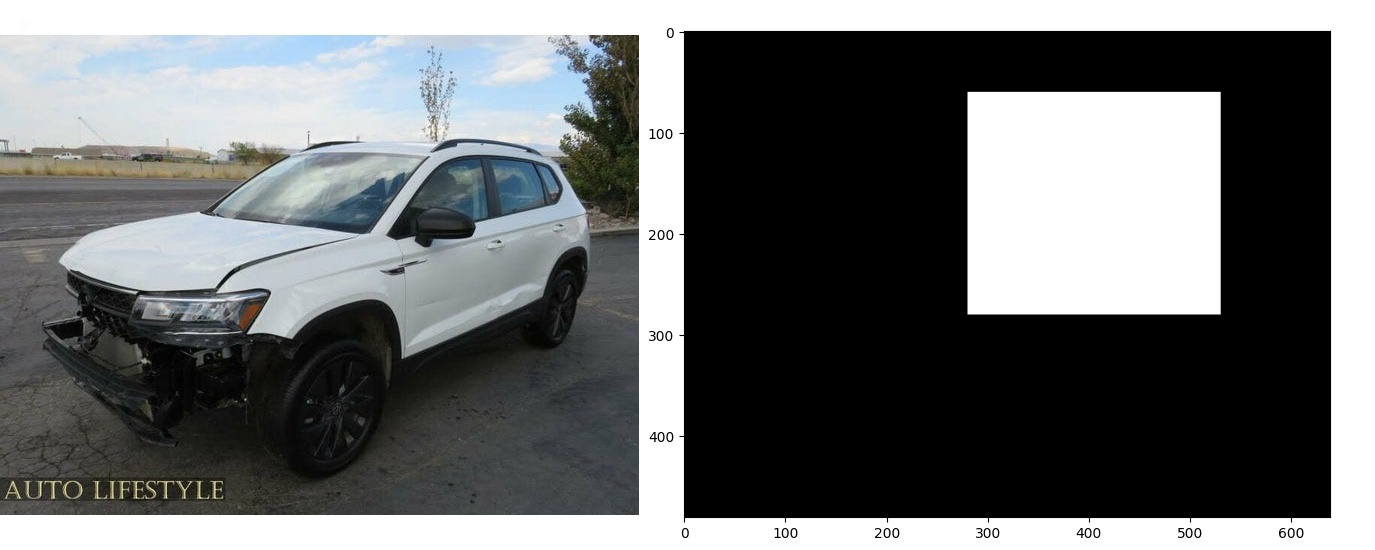
Upon further exploration of the data analysis process, I uncovered additional inconsistencies. Particularly, I observed that the images in the online dataset predominantly focused on the damaged section of the vehicle, while the images obtained through web scraping depicted intact cars in their entirety. To address this disparity, I employed normalization techniques such as cropping the images to a square shape, zooming in on the central area, and resizing them to ensure uniformity. By normalizing and organizing the data, I successfully overcame the most difficult initial phase of the project.

Technical Approach

In designing my damage detection model, I chose to utilize a highly effective design called U-net CNN architecture. This model consists of four convolutional blocks, which downsample and upsample the input image to create a segmentation map. It’s called a U-net because the graphical structure of the convolutional blocks makes the most sense in a “u” shape. At each scale, the model extracts and combines features to enable accurate identification of damage.

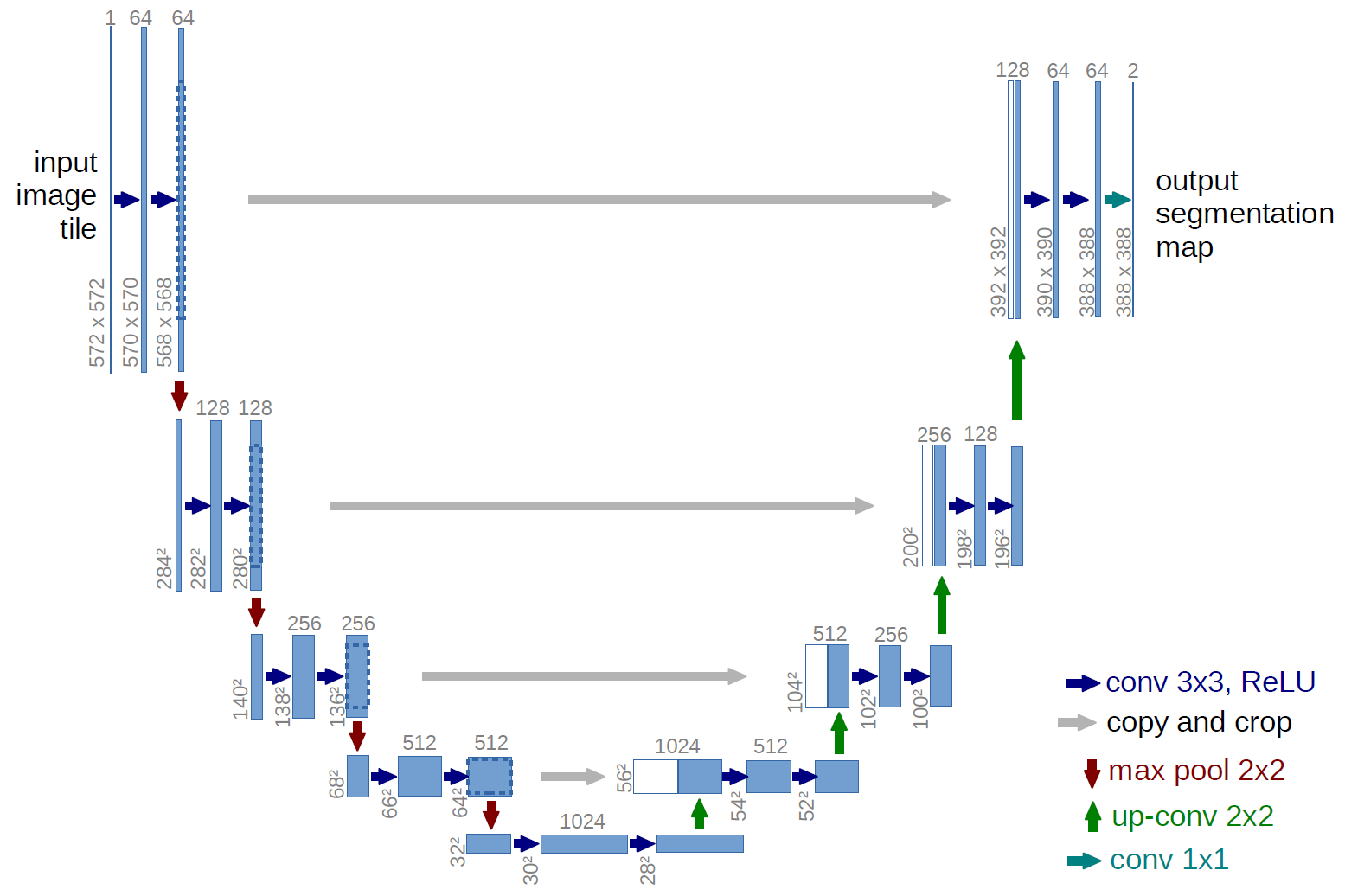
Each downsampling block is composed of four layers, which apply convolution, batch normalization, and ReLU to progressively increase the number of channels from three to 256, while reducing the spatial dimensions of the output through max pooling. The upsampling blocks use four layers as well, but utilize transposed convolution to increase the spatial dimensions of the input. Furthermore, each layer reduces the number of output channels by half while doubling the input channels with skip connections. Theses connections preserve much of the original, unconvoluted information from the image further down in the neural net, which makes training much easier.

                            
class DamageDetection(nn.Module):
  def __init__(self):
    super(DamageDetection, self).__init__()
    # Downsample convolution blocks
    self.dblock1 = ConvBlock(3, 32)
    self.dblock2 = ConvBlock(32, 64)
    self.dblock3 = ConvBlock(64, 128)
    self.dblock4 = ConvBlock(128, 256)
    # Upsample convolution blocks
    self.ublock1 = ConvBlock(256, 512, True)
    # The next 4 blocks have doubled input channels due to concatenation of skip connections
    self.ublock2 = ConvBlock(512, 256, True)
    self.ublock3 = ConvBlock(256, 128, True)
    self.ublock4 = ConvBlock(128, 64, True)
    # Output "block"
    self.convf1 = nn.Conv2d(64, 32, (3,3), padding=(1,1))
    self.convf2 = nn.Conv2d(32, 32, (3,3), padding=(1,1))
    self.convf3 = nn.Conv2d(32, 2, (1,1), padding=(0,0))

    self.down = nn.MaxPool2d(2)
 
  def forward(self, input):
    # Save the last feature maps on each level! Pass an instance forward, but keep the variable referencing the same feature map for concatenation
    l1 = self.dblock1(input)
    l2 = self.dblock2(self.down(l1))
    l3 = self.dblock3(self.down(l2))
    l4 = self.dblock4(self.down(l3))
    # Concatinate l1 - l4 on inputs across the U in reverse order, matching sizes
    u = self.ublock1(self.down(l4))
    u = self.ublock2(torch.cat((l4, u), dim=1))
    u = self.ublock3(torch.cat((l3, u), dim=1))
    u = self.ublock4(torch.cat((l2, u), dim=1))
    out = F.relu(self.convf1(torch.cat((l1, u), dim=1)))
    out = F.relu(self.convf2(out))
    out = self.convf3(out)
    return out
                            
                        

Here's the ConvBlock object for reference:

                            
class ConvBlock(nn.Module):
  def __init__(self, in_channels, out_channels, up_sample=False):
    super(ConvBlock, self).__init__()
    self.conv1 = nn.Conv2d(in_channels, out_channels, (3,3), padding=(1,1))
    self.conv2 = nn.Conv2d(out_channels, out_channels, (3,3), padding=(1,1))
    self.up_sample = up_sample
    if up_sample:    
      # Up sample with up-conv 2x2, doubling along each dimension
      self.up = nn.ConvTranspose2d(out_channels, out_channels//2, 2, stride=2)
    # We do not want to down sample in the block, since we need the non-down-sampled output for skip connections

  def forward(self, input):
    x = F.relu(self.conv1(input))
    x = F.relu(self.conv2(x))
    if self.up_sample:
      x = self.up(x)
    return x
                            
                        

As I mentioned earlier, I discovered through a process of trial and error that rather than annotating images with the specific location of damage didn’t work well. Instead, my model performed better when images were labeled as either damaged or undamaged with corresponding masks of all ones or all zeros. This approach allowed the model to discern damage location and severity on its own, without relying on exact damage location annotations for all 3,000 images.

Results

After twenty rigorous epochs, the damage detection model reached an impressive level of proficiency. By the fifth epoch, the model was already able to detect the overall shape of cars with reasonable accuracy and identified damaged areas in images. As the model continued training, its accuracy steadily improved until it plateaued around the 16th epoch, achieving a remarkable accuracy of 93% in pinpointing the location of damage in an image.

However, it's worth noting that this accuracy pertains solely to the detection of specific damaged areas in an image, while the accuracy of distinguishing between clean and damaged cars soared to nearly 99%. Although the final error rate in detecting the location of damage on an image was around 20%, the model still performed remarkably well in detecting damage in images with high accuracy and considerable proficiency in identifying the general shape of cars. As a side note, you’ll be happy to hear that I got a 100 on the final project so it all worked out in the end. If you'd like to see more of the code for this project, you can find it all on my GitHub.

Limitless Applications

As you can tell, deep learning is an incredibly captivating application of mathematics that has opened up a world of astonishing possibilities. By utilizing principles from linear algebra, calculus, and probability theory, models like this one can effectively process vast amounts of data and extract meaningful insights. This powerful combination of math and data has led to all kinds of other impressive use cases such as learning intricate patterns to identify diseases and help with medical diagnoses.

These models employ convolutional neural networks (CNNs) to capture spatial features in the images and recurrent neural networks (RNNs) to analyze sequential data such as patient histories. The diverse applications of deep learning continue to demonstrate the incredible potential of combining mathematics and artificial intelligence, and I was thrilled by the opportunity I had to explore even one use case. If you’d like to learn more, visit my GitHub to view the full repository.